Algorithmique de la mobilité

↑ Accueil du cours

Voyageur de commerce euclidien (1-L'interface)

Le problème du voyageur de commerce (TSP pour traveling salesman problem) consiste, en termes simples, à visiter un ensemble de lieux en minimisant le coût total de déplacement. Dans sa variante euclidienne, les lieux sont des coordonnées en deux dimensions (points) et le coût pour aller d'un lieu à un autre est la distance euclidienne (classique) entre leurs points.

Dans cette première partie, nous mettons en place une interface graphique permettant à l'utilisateur d'ajouter des points d'intérêts avant de déclencher l'algorithme de TSP. Nous décrivons également les méthodes qui nous permettront plus tard de dessiner le parcours ou de l'affecter à un noeud de type WaypointNode(fichier ici). Ceci est fait dans les classes Java suivantes (expliquées plus bas) :

Classe Target

Afin de permettre à l'utilisateur d'ajouter ou d'enlever à la souris de nouveaux points à visiter, nous matérialisons ces derniers par une nouvelle classe de noeuds: Target.

import io.jbotsim.core.Node;
import io.jbotsim.ui.icons.Icons;

public class Target extends Node {
    public Target() {
        disableWireless();
        setIcon(Icons.PLUS);
    }
}

La classe Target hérite de la classe Node. Son fonctionnement ne diffère que très peu de sa classe mère et est relativement simple :

Classe Controller

La classe Controller, comme son nom l'indique, est le composant clé qui articule les éléments nécessaires pour faire tourner l'algorithme et sa visualisation. 

import io.jbotsim.core.Node;
import io.jbotsim.core.Point;
import io.jbotsim.core.Topology;
import io.jbotsim.core.event.CommandListener;
import io.jbotsim.ui.JTopology;
import io.jbotsim.ui.JViewer;
import io.jbotsim.ui.painting.BackgroundPainter;
import io.jbotsim.ui.painting.UIComponent;

import java.awt.*;
import java.util.ArrayList;
import java.util.List;
import java.util.Collections;

public class Controller implements CommandListener, BackgroundPainter {

    public static final String COMMAND_COMPUTE_TSP = "Compute TSP";

    private Topology topology;
    private JTopology jTopology;

    private List<Point> points = new ArrayList<>();

    public Controller() {
        topology = new Topology();
        topology.setDefaultNodeModel(Target.class);

        jTopology = new JTopology(topology);
        jTopology.addBackgroundPainter(this);

        new JViewer(jTopology);

        // Adding the custom command after the creation of
        // the JViewer makes sure it is displayed last.
        topology.addCommand(COMMAND_COMPUTE_TSP);
        topology.addCommandListener(this);
    }

    @Override
    public void onCommand(String command) {
        if (command.equals(COMMAND_COMPUTE_TSP)) {
            points.clear();
            for (Node node : topology.getNodes())
                if (node instanceof Target)
                    points.add(node.getLocation());

            List<Point> itinerary = computeItinerary(points);

            points = itinerary; // For drawing purposes

            assignToNode(itinerary);
        }
    }

    protected List<Point> computeItinerary(List<Point> points) {
        // TODO replace this code by a call to your algorithm
        List<Point> itinerary = new ArrayList<>(points);
        Collections.shuffle(itinerary); 
        return itinerary;
    }

    @Override
    public void paintBackground(UIComponent c, Topology tp) {
        Graphics2D g2d = (Graphics2D) c.getComponent();
        for (int i = 0; i < points.size(); i++) {
            Point from = points.get(i);
            Point to = points.get((i + 1) % points.size());
            g2d.drawLine((int) from.getX(), (int) from.getY(),
                    (int) to.getX(), (int) to.getY());
        }
    }

    protected void assignToNode(List<Point> itinerary) {
        if (!itinerary.isEmpty()) {
            WaypointNode node = new WaypointNode();
            node.setLocation(itinerary.get(0));
            for (int i = 1; i < itinerary.size() + 1; i++)
                node.addDestination(itinerary.get(i % itinerary.size()));
            topology.addNode(node);
        }
    }
}

Liste de points à visiter

La liste des points à visiter est gardée dans le champs points ci-dessous.

      private List<Point> points = new ArrayList<Point>();

Dans le constructeur, en faisant de Target le modèle de noeud par défaut de la Topology, on permet à l'utilisateur d'ajouter/enlever des points d'intérêts à la souris:

      topology.setDefaultNodeModel(Target.class);

Ces points seront transférés plus tard de la Topology vers la liste points.

Ajout d'une commande dans le menu contextuel

Une commande a été ajoutée au menu contextuel, afin de permettre à l'utilisateur de démarrer le TSP une fois que les points sont ajoutés, comme illustré ci-dessous.

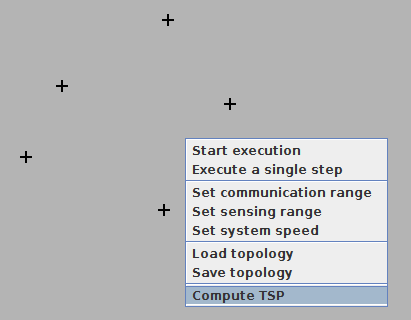
Pour ce faire, nous avons appelé la méthode addCommand() de la classe Topology depuis notre constructeur, avec comme paramètre l'intitulé du menu (ici "Compute TSP", placé dans une constante).

        topology.addCommand(COMMAND_COMPUTE_TSP);

Nous avons enregistré ensuite notre objet via addCommandListener() sur la Topology afin qu'il soit notifié lorsqu'une commande est sélectionnée. 

        topology.addCommandListener(this);

Enfin, nous avons implémenté la méthode correspondante de l'interface CommandListener, à savoir onCommand(), qui teste si la commande cliquée est bien "Compute TSP" et récupére la liste des points présents dans la Topology qui sont de type Target pour les ajouter à la liste de points. Cela correspond à l'extrait de code suivant (présent dans la classe Controller).

    @Override
    public void onCommand(String command) {
        if (command.equals(COMMAND_COMPUTE_TSP)) {
            points.clear();
            for (Node node : topology.getNodes())
                if (node instanceof Target)
                    points.add(node.getLocation());
    ...

Dessin de l'itinéraire

Les algorithmes de TSP que nous allons coder consisteront à ré-ordonner la liste de points de la meilleure manière possible. Afin de visualiser le résultat de ces algorithmes (comme à la figure ci-dessous), nous redéfinissons la façon dont JBotSim dessine le fond de la topologie en y ajoutant le dessin de l'itinéraire.

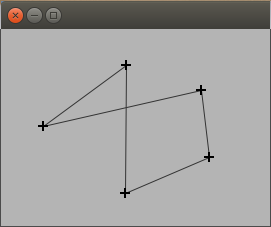
Le composant graphique responsable de dessiner une topologie dans JBotSim est la JTopology. En général, elle est créée automatiquement par le JViewer (qui l'encapsule et rajoute le fenêtrage). Ici, nous l'avons créé manuellement pour en modifier le BackgroundPainter (c.f. le code du constructeur Controller() ci-dessus). Ainsi, notre classe Controller, qui implémente bien l'interface BackgroundPainter, s'enregistre via la méthode addBackgroundPainter() auprès de la JTopology. Le code correspondant, placé dans BackgroundPainter.paintBackground() consiste à dessiner les segments correspondants à l'itinéraire.

    @Override
    public void paintBackground(UIComponent c, Topology tp) {
        Graphics2D g2d = (Graphics2D) c.getComponent();
        for (int i = 0; i < points.size(); i++) {
            Point from = points.get(i);
            Point to = points.get((i + 1) % points.size());
            g2d.drawLine((int) from.getX(), (int) from.getY(),
                    (int) to.getX(), (int) to.getY());
        }
    }

Affectation du parcours à un noeud

Enfin, la méthode assignToNode() permet d'affecter une liste de points à visiter à un noeud de type WaypointNode. Si vous n'avez pas cette classe, vous pouvez suivre la leçon correspondante ou bien télécharger le fichier directement.

Le noeud est créé et placé sur la première position du parcours. Les points d'intérêts sont ajoutés séquentiellement, en terminant par le premier. 

    protected void assignToNode(List<Point> points) {
        if (!points.isEmpty()) {
            WaypointNode node = new WaypointNode();
            node.setLocation(points.get(0));
            for (int i = 1; i < points.size() + 1; i++)
                node.addDestination(points.get(i % points.size()));
            topology.addNode(node);
        }
    }

assignToNode() est appelée dans onCommand(), juste après que nous ayons calculé l'ordre de visite (itinerary).

Classe MainTSP

La classe MainTSP comporte simplement un main qui crée un Controller.

public class MainTSP {
    public static void main(String[] args) {
        new Controller();
    }
}

Dans la version fournie, le noeud parcourt les points dans leur ordre de création. N'oubliez pas de cliquer sur "Start execution" dans le menu contextuel pour démarrer le parcours, après avoir calculé le TSP.

Voyageur de commerce euclidien (2-Les algorithmes)

Nous nous concentrons maintenant sur les algorithmes eux-mêmes.

Le problème du TSP est NP-difficile, et ce même dans sa variante euclidienne. On étudiera ici des algorithmes d'approximation, c.à.d. qui fournissent des solutions non-optimales, mais calculées rapidement (voire très rapidement).

Algorithme naïf

La classe Algorithm ci-dessous nous servira de base pour nos différentes versions de l'algorithme. Elle comporte:

import io.jbotsim.core.Point;

import java.util.List;

public class Algorithm {

    protected List<Point> points;

    public void setPoints(List<Point> points){
        this.points = points;
    }

    public List<Point> getItinerary(){
        List<Point> itinerary = new ArrayList<>();
        // TODO compute itinerary from the points
        return itinerary;
    }
}

Pour cette première implémentation naïve, l'itinéraire renvoyé est simplement la liste de points à visiter, sans plus de traitement. Pour la suite, c'est getItinerary() qu'il faudra modifier/surcharger en fonction des algorithmes implémentés.

Maintenant que nous avons créé la classe Algorithm nous pouvons remplacer le TODO dans Controller.computeItinerary() par le code suivant:

    Algorithm algorithm = new Algorithm();
    algorithm.setPoints(points);
    List<Point> itinerary = algorithm.getItinerary();

Le comportement devrait être le même que précédement.

Conception et implémentation d'algorithme

Q1. Nous avons discuté en classe de plusieurs algorithmes, par exemple :

  1. Nearest neighbor
  2. Random insertion
  3. 2-approx (based on MST)
  4. Brute force (⚠factoriel, déconseillé)

Codez-en un ou deux (de votre choix) en comparant leurs performances. Privilégiez d'abord la simplicité, avant de vous lancer dans des algorithmes compliqués.

Évaluation de la qualité : Le coût total d'un itinéraire est la somme des longueurs de ses segments (en incluant le retour au point initial). Afin de tester la qualité de votre algorithme, nous vous proposons les deux jeux de test suivants dans une surface de 600x400. La solution optimale pour le premier d'entre eux a une distance totale de 1631,527 (arrondi). La solution optimale pour le second n'est pas connue... À chaque fois que vous battez le record, nous l'écrirons au tableau ;-)

Jeu de données 1 :

   topology.addNode(58.0, 128.0);
   topology.addNode(157.0, 51.0);
   topology.addNode(224.0, 150.0);
   topology.addNode(339.0, 68.0);
   topology.addNode(460.0, 39.0);
   topology.addNode(537.0, 150.0);
   topology.addNode(568.0, 358.0);
   topology.addNode(458.0, 306.0);
   topology.addNode(222.0, 353.0);
   topology.addNode(113.0, 289.0);
   topology.addNode(437.0, 119.0);
   topology.addNode(360.0, 280.0);
   topology.addNode(128.0, 219.0);
   topology.addNode(271.0, 81.0);
   topology.addNode(504.0, 222.0);

Jeu de données 2 :

    topology.addNode(591.0, 229.0);
    topology.addNode(548.0, 99.0);
    topology.addNode(396.0, 255.0);
    topology.addNode(531.0, 79.0);
    topology.addNode(476.0, 263.0);
    topology.addNode(322.0, 332.0);
    topology.addNode(519.0, 10.0);
    topology.addNode(234.0, 381.0);
    topology.addNode(43.0, 72.0);
    topology.addNode(271.0, 56.0);
    topology.addNode(406.0, 152.0);
    topology.addNode(574.0, 174.0);
    topology.addNode(382.0, 245.0);
    topology.addNode(161.0, 297.0);
    topology.addNode(361.0, 362.0);
    topology.addNode(104.0, 155.0);
    topology.addNode(466.0, 44.0);
    topology.addNode(342.0, 10.0);
    topology.addNode(252.0, 35.0);
    topology.addNode(321.0, 136.0);