Maintenance d'une forêt d'arbres couvrants

Quand la mobilité est forte, il est fréquent que le réseau se retrouve partitionné en plusieurs composantes connexes. Dans ce cas là, le problème classique de l'arbre couvrant revient à tenter de maintenir plusieurs arbres couvrants (on parle donc d'une forêt), avec idéalement un seul arbre par composante connexe, comme illustré ci-dessous.

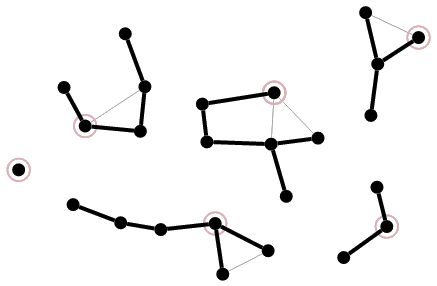
Un tel algorithme ne termine jamais. Lorsque des composantes se rejoignent, on veut que leurs arbres fusionnent pour ne faire qu'un. De même, quand une composante se sépare en plusieurs morceaux, on veut garantir que chaque morceau possède un arbre valide.

L'algorithme

Nous considérons maintenant un tel algorithme. Son comportement peut être visionné sur cette vidéo. L'algorithme se présente sous la forme d'un protocole de population d'un genre un peu spécial, avec trois règles expliquées ci-dessous. Les noeuds peuvent être dans deux états : l'état R si le noeud est la racine de son arbre, et N sinon (vous pouvez utiliser des couleurs à la place). Initialement, tous les noeuds sont dans l'état R car ils forment chacun un arbre de cardinalité 1 (dont ils sont la racine). Voici les trois règles de l'algorithme.

1. Une règle de fusion (): si deux racines d’arbres interagissent, l’une des deux est supprimée et les deux arbres sont fusionnés en mettant en gras l’arête correspondante (désactiver le setWidth() de l’ordonnanceur pour éviter les conflits). Le lien avec un voisin donné peut être obtenu via la méthode getCommonLinkWith(). Il faudra également utiliser une variable parent de type Node pour mémoriser qui est notre parent dans l'arbre. Par convention, on dira que la racine d'un arbre est son propre parent (this). Lorsqu'une fusion a lieu, le noeud qui n'est plus racine choisi l'autre comme parent.

2. Une règle de circulation (), consistant à faire circuler la racine au sein de son propre arbre, en inversant la relation parent/enfant locale à chaque mouvement. Attention : cette règle ne doit s'appliquer que si le sommet R est le parent du sommet N.

3. Une règle de régénération (), qui consiste à régénérer une racine sur un nœud si l'arête menant à son parent vient de disparaitre. Cette règle est d'un type différent car elle ne dépend pas de l'ordonnanceur. Elle dépend des changements topologiques dans le réseau et constitue une réaction à ces derniers (discuté ci-dessous).

Implémentation

Les deux premières règles peuvent être implémentées de la même manière qu'un protocole de population classique (c.f. cours précédent). La troisième règle est une réaction à la disparition d'un lien local, on la code donc différemment. Dans JBotSim, un noeud peut réagir à la disparition d'un lien en redéfinissant la méthode onLinkRemoved() (héritée de la classe Node). Le code reviendra à tester, dans cette méthode, si le lien qui a disparu mène vers le noeud parent. Si oui, on redevient racine.