Vector Racer

Nous allons adapter les algorithmes vus pour le robot, pour une autre entité mobile, un drone.

↓

Exemple d'une entité mobile Vector Racer, et d'un algorithme de recherche de chemin avec obstacles.

Pour construire un espace des configurations nous supposons :

Le drone peut modifier sa vitesse de 10 dans la dimension est-ouest chaque unité de temps.
Le drone peut également modifier sa vitesse de 10 dans la dimension nord-sud chaque unité de temps.
Il existe un endroit $(t_x, t_y)$ accessible au drone, tel que la cible est considérée visitée si le drone est sur $(t_x, t_y)$ à n'importe quelle vitesse.
Le drone se trouve initialement sur $(d_x, d_y)$ à vitesse nulle, avec $d_x$, $d_y$ des multiples de 10.

Q1. Ces capacités de l'entité mobile viennent d'un jeu mathématique, nommé entre autres Vector Racer, Racetrack, etc.. Jouez quelques jeux sur https://harmmade.com/vectorracer/, jusqu'à ce que vous compreniez bien les règles et surtout les contraintes de déplacement du drone. Il est possible de jouer à plusieurs, ou même de jouer sur une feuille quadrillée en déssinant son propre parcours.

Remarque : Ces simples règles créent également des forces d'inertie, c'est à dire, il est dur de changer brusquement de vitesse (voir image ci-dessous).

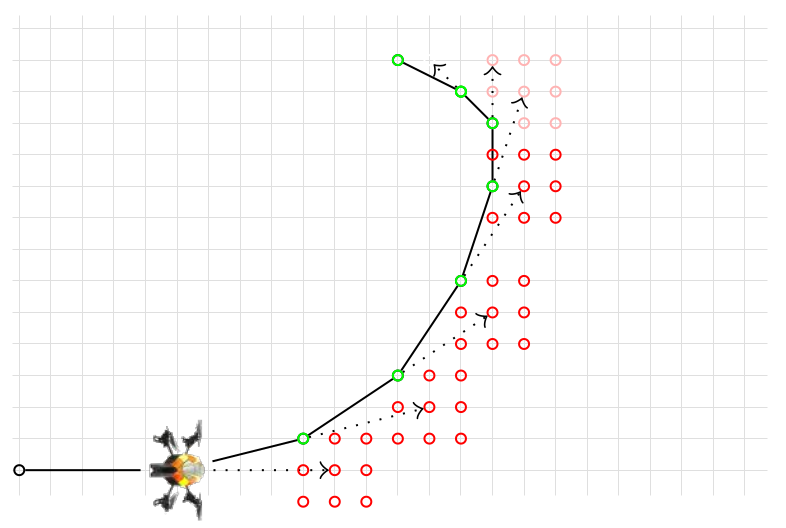
Exemple d'une trajectoire obéissant aux contraintes de mobilité du drone (ou de Vector Racer). En rouge, on a les choix possibles à chaque étape, avec en vert, l'endroit choisi.

Implémentation avec JBotSim

Chaque configuration possible du drone peut être représentée par un tuple $(x, y, dx, dy)$, où $x$ et $y$ représentent les coordonnées dans le plan du drone (comme pour le robot) et $dx$ et $dy$ représentent la vitesse du drone. La configuration du départ est donc notée $(d_x, d_y, 0, 0)$. Après 1 unité de temps, le drone pourrait se trouver à neuf configurations distinctes, notamment $(d_x, d_y, 0, 0)$, la configuration dans laquelle le drone n'accélère dans aucune des deux dimensions, $(d_x + 10, d_y, 10, 0)$ et $(d_x, d_y + 10, 0, 10)$, les configurations du drone s'il n'accélère que dans la dimension x (est-ouest), $(d_x - 10, d_y, -10, 0)$ et $(d_x, d_y - 10, 0, -10)$, si le drone n'accélère que dans la dimension $y$ (nord-sud), et $(d_x + 10, d_y + 10, 10, 10)$, $(d_x + 10, d_y - 10, 10, -10)$, $(d_x - 10, d_y + 10, -10, 10)$, et $(d_x - 10, d_y - 10, -10, -10)$, les configurations quand le drone accélère dans les deux dimensions. On crée alors huit nouveaux sommets dans l'espace des configurations représentant les huit nouvelles configurations (pas neuf, car $(d_x, d_y, 0, 0)$ a déjà un sommet correspondant dans l'espace des configurations), et on crée des arcs du sommet de départ vers chacun de ces huit nouveaux sommets. Ce processus se répète alors pour les nouveaux sommets. Prenons le sommet représentant la configuration $(d_x + 10, d_y, 10, 0)$. Les prochaines configurations possibles à partir de celle-ci sont $(d_x + 20, d_y, 10, 0)$, $(d_x + 30, d_y, 20, 0)$, $(d_x + 10, d_y, 0, 0)$, $(d_x + 20, d_y + 10, 10, 10)$, $(d_x + 20, d_y - 10, 10, -10)$, $(d_x + 30, d_y + 10, 20, 10)$, $(d_x + 30, d_y - 10, 20, -10)$, $(d_x + 10, d_y + 10, 0, 10)$, $(d_x + 10, d_y - 10, 0, -10)$. On rajoute tous ces neuf nouveaux sommets car aucune de ces configurations est déjà présente dans l'espace des configurations. On lie ces sommets avec des arcs à partir de $(d_x + 10, d_y, 10, 0)$. En continuant ce processus, on observe bien que l'espace créé correspond en fait à $(10x, 10y, 10dx, 10dy)$, pour tout $x$, $y$, $dx$ et $dy$ entiers, avec des arcs de toute configuration $(x, y, dx, dy)$ vers $(x', y', dx', dy')$ si $x + dx' = x'$ et $y + dy' = y'$ et $|dx' - dx| \leq 10$ et $|dy' - dy| \leq 10$. La cible se trouve dans cet espace, sous forme de plusieurs sommets de la forme $(t_x, t_y, dx, dy)$, pour tout $dx$ et $dy$.

Voici les classes nécessaires :

Configuration4D class

package drone;

import io.jbotsim.core.Point;

public class Configuration4D extends Point {

    private Configuration4D parent;
    private double dx;
    private double dy;

    public Configuration4D(double x, double y, double dx, double dy, Configuration4D parent){
        super(x, y);
        this.parent = parent;
        this.dx = dx;
        this.dy = dy;
    }

    public double getDx(){
        return dx;
    }

    public double getDy(){
        return dy;
    }

    public Configuration4D getParent() {
        return parent;
    }

    @Override
    public boolean equals(Object obj) {
        if (obj instanceof Configuration4D){
            Configuration4D p = (Configuration4D) obj;
            return this.getX() == p.getX()
                    && this.getY() == p.getY()
                    && this.getDx() == p.getDx()
                    && this.getDy() == p.getDy();
        }
        return false;
    }
}

Drone class

package drone;

import drone.algorithms.*;
import environment.GridNode;
import io.jbotsim.ui.icons.Icons;

import java.util.ArrayList;

public class Drone extends GridNode {

    private ArrayList<Configuration4D> trajectory;
    private int trajectoryIterator;
    private double speed;
    private SearchAlgorithm searchAlgo;

    public Drone(){
        setIcon(Icons.DRONE);
        setIconSize((int)(getIconSize()*1.5));
        trajectory = new ArrayList();
        trajectoryIterator = 1;
        speed = 2.5;
    }

    @Override
    public void onStart() {
        super.onStart();
        searchAlgo = new BFS(this); //<--------------------------change the search algorithm
        searchAlgo.onStart();
    }

    @Override
    public void onClock() {
        super.onClock();
        if(trajectory.isEmpty()) {
            searchAlgo.onClock();
        } else {
            followTrajectory();
        }
    }

    private void followTrajectory() {
        if (trajectoryIterator < trajectory.size()) {
            Configuration4D prev = trajectory.get(trajectoryIterator-1);
            Configuration4D next = trajectory.get(trajectoryIterator);
            double dist = prev.distance(next) / resolution;
            setDirection(next);
            move(speed * dist);
            if (distance(next) < speed){
                trajectoryIterator++;
            }
        }
    }

    public ArrayList<Configuration4D> getTrajectory(){
        return trajectory;
    }

    public void setTrajectory(ArrayList<Configuration4D> list){
        trajectory = list;
    }

    public SearchAlgorithm getSearchAlgo(){
        return searchAlgo;
    }
}

SearchAlgorithm class

package drone.algorithms;

import environment.Fire;
import environment.Target;
import io.jbotsim.core.Node;
import io.jbotsim.core.Topology;
import drone.Configuration4D;
import drone.Drone;

import java.util.ArrayList;
import java.util.Collections;

public abstract class SearchAlgorithm {

    protected Configuration4D start;
    protected Configuration4D target = new Configuration4D(0, 0, 0, 0, null);
    protected ArrayList<Configuration4D> searchHistory;
    protected Drone d;

    public void onStart() {
        start = new Configuration4D(d.getX(), d.getY(), 0, 0, null);
        for (Node n : d.getTopology().getNodes()) {
            if (n instanceof Target) {
                ((Target) n).reposition();
                target = new Configuration4D(n.getX(), n.getY(), 0, 0, null);
            }
        }
    }

    public abstract void onClock();

    public SearchAlgorithm(Drone d) {
        this.d = d;
        searchHistory = new ArrayList();
    }

    protected boolean valid(Configuration4D current) {
        // Testing if passed through fire
        Topology tp = d.getTopology();
        Configuration4D parent = current.getParent();
        if (parent != null) {
            for (Node fire : tp.getNodes()) {
                if (fire instanceof Fire) {
                    if (fire.distance(current) + fire.distance(parent) 
                        <= current.distance(parent) + Fire.safetyDistance) {//passed fire
                        return false;
                    }
                }
            }
        }
        //Testing if out of bounds
        double x = current.getX();
        double y = current.getY();
        if (x <= 0 || y <= 0 || x >= tp.getWidth() || y >= tp.getHeight()) { 
            return false;
        }
        return true; //valid
    }

    protected boolean foundTarget(Configuration4D current) {
        if (current.getX() == target.getX() && current.getY() == target.getY()){
            return true;
        }
        return false;
    }

    protected void retraceTrajectory(Configuration4D p) {
        ArrayList<Configuration4D> result = new ArrayList<>();
        result.add(p);
        while (p.getParent() != null) {
            p = p.getParent();
            result.add(p);
        }
        Collections.reverse(result);
        d.setTrajectory(result);
    }

    public ArrayList<Configuration4D> getSearchHistory() {
        return searchHistory;
    }
}

Q3. Commencez par adapter la classe principale Environment, pour pouvoir rajouter des noeuds Drone, et pour pouvoir visualiser leur algorithme de recherche. Ceci se fait naturellement (copier, coller et adapter).

Q3. Codez l'algorithme de parcours en largeur pour le drone. L'adaptation à partir de celui pour le robot se fait naturellement, il suffit de changer le robot en drone, les configurations robot en configurations drone, et de créer les neuf configurations enfants, au lieu des quatre pour le robot. Exécutez Environment pour tester votre drone.

Q4. Lancez l'algorithme de parcours en largeur dans l'environnement 2. Vous remarquerez que, par rapport au robot, on a un calcul beaucoup plus long. Ceci est dû au fait que le drone a beaucoup plus de configurations possibles à tester. Dans le pire cas, combien de configurations estimez-vous qu'il puisse y avoir dans notre espace de taille $600 \times 400$ ? Rappelez-vous que le drone ne puisse prendre que des états de la forme $(10x, 10y, 10dx, 10dy)$. En général, combien d'états cela fait dans un espace de taille $n \times n$ ?

Q5. Supposons que le point de départ est $(0,0)$, et le point d'arrivée $(3, 0)$. À partir d'une vitesse nulle et en accélérant toujours vers le point d'arrivée, il faudra 2 unités de temps avant de pouvoir l'atteindre.

Supposons le point d'arrivée $(10,0)$. Combien d'unités de temps faudra-t-il pour atteindre (ou dépasser) le point d'arrivée ?
Même question, mais en considérant maintenant une vitesse de départ de $(5, 0)$ ?
Même question, mais en considérant maintenant une vitesse de départ de $(-3, 0)$ ?
Même question, mais en considérant maintenant une vitesse de départ de $(-3, 25)$ ?
Même question, en considérant comme point d'arrivée $(10, 5)$, vitesse de départ $(0, 0)$ ? Une astuce est de considérer la question dans les deux dimensions séparément.
Finalement, en considérant comme point d'arrivée $(10, 5)$, vitesse de départ $(0, 0)$ et des obstacles, combien d'unités de temps il faut au minimum ?

Q6. Avant de coder l'algorithme A étoile pour le drone, réfléchissez à une fonction d'estimation en vous inspirant de la dernière question.

Q7. Codez l'algorithme A étoile pour le drone, en vous inspirant fortement de celui pour le robot, et en utilisant la fonction d'estimation de Q5.

Q8 (bonus). Codez l'algorithme A étoile bidirectionnelle pour le drone. La difficulté par rapport à celui pour le robot, est qu'il faut faire attention à quand on peut coller les deux bouts de chemin. En effet, il va falloir non seulement vérifier si on est sur une même position, mais vérifier si les vitesses collent bien également, parce que le drone a du mal à tourner brusquement.

Q9 (bonus). Prouvez pourquoi nos algorithmes de parcours en largeur retournent un chemin optimal. Une preuve par contradiction serait le plus simple. Autrement dit, supposez que le chemin retourné n'est pas optimal, puis montrez en quoi ceci crée une contradiction. Il est peut-être plus facile d'avoir l'intuition en regardant l'algorithme sur des exemples avec le robot.

La preuve d'optimalité de A étoile est bien plus compliquée (https://en.wikipedia.org/wiki/A*_search_algorithm#Admissibility). L'important à savoir est que tant que l'heuristique d'estimation ne sur-estime pas, alors l'optimalité est garantie. On peut remarquer d'ailleurs que si la fonction d'estimation est simplement 0, alors l'optimalité est garanti également, car ceci reviendrait simplement à l'algorithme de Dijkstra (qui a, dans notre cas, le même comportement que l'algorithme de parcours en largeur).