Recherche de chemin
Le calcul de trajectoire, ou encore recherche de chemin (pathfinding), est un problème associé à l'intélligence artificielle et à la plannification, souvent utilisé pour se déplacer dans les jeux vidéos. Le but est de calculer un chemin pour une entité autonome, entre un point de départ et un point d'arrivée donnés, dans un environnement avec ou sans obstacles.
Nous allons apprendre et coder quelques algorithmes de recherche de chemin utilisant l'espace des configurations.

↓

↓

Exemple d'une instance et d'un algorithme de recherche de chemin avec obstacles.
Espace des configurations
Un espace des configurations est un graphe orienté. Les sommets représentent toutes les configurations possibles que puisse prendre l'entité autonome. Un arc d'un sommet $c1$ à un sommet $c2$ représente la possibilité de l'entité autonome de changer sa configuration $c1$ en $c2$ en une seule unité de temps.
Algorithmes de recherche
Comme l'espace des configurations est un graphe, nous allons simplement utiliser des algorithmes de recherche des graphes ! Il existe plusieurs algorithmes, dont la marche aléatoire, le parcours en profondeur, etc. Nous nous concentrons directement sur des algorithmes résultants dans un chemin optimal :
- Parcours en largeur (breadth first search ou BFS en anglais) : On cherche un chemin en parcourant d'abord les noeuds proches du noeud de départ, en s'éloignant de plus en plus de ce noeud de départ.
- A étoile (A* ou A star en anglais) : On guide le parcours en largeur dans une bonne direction à l'aide d'une heuristique d'estimation.
- A étoile bidirectionnel : On exécute deux algorithmes A étoile , un à partir du noeud de départ, l'autre à partir du noeud d'arrivée. Dès que des branches des deux A étoile , se touchent, on construit le chemin en liant les deux bouts de chemin correspondants.
Implémentation avec JBotSim
Faisons en sorte que chaque noeud, comme la cible ou l'entité mobile, ajouté dans la topologie soit déplacé automatiquement sur le point le plus proche d'une grille d'une résolution donnée (ici 10), avec la classe GridNode. Ceci est fait seulement pour nous simplifier les algorithmes ensuite. Ces noeuds de la topologie JBotSim ne sont pas à confondre dans la suite avec les sommets de l'espace des configurations !
GridNode class
package environment;
import io.jbotsim.core.Node;
public class GridNode extends Node {
public static double resolution = 10.0; //<----------------------change resolution here
public GridNode(){
setWirelessStatus(false);
}
@Override
public void onStart() {
super.onStart();
reposition();
}
@Override
public void onClock() {
super.onClock();
setLocation(getLocation()); //force graphic update
}
public void reposition() {
double newX = Math.round(getX()/resolution)*resolution;
double newY = Math.round(getY()/resolution)*resolution)
setLocation(newX, newY);
}
public double getResolution(){ return resolution; }
}IntelliJ devrait vous prévenir que le paquet environment n'existe pas. Utilisez alors les touches magiques Alt + Entrée sur le mot environment pour créer ce paquet. Vous allez devoir le faire plusieurs fois dans la suite.
Notre cible est faite à l'aide de la classe Target;
Target class
package environment;
import io.jbotsim.ui.icons.Icons;
public class Target extends GridNode {
public Target(){
setIcon(Icons.FLAG);
setIconSize((int)(getIconSize()*1.5));
}
}et nos obstacles à l'aide de la classe Fire.
Fire class
package environment;
import io.jbotsim.ui.icons.Icons;
public class Fire extends GridNode {
public static double safetyDistance = 25.0;
public Fire(){
setIcon(Icons.FIRE);
setIconSize((int)(getIconSize()*1.3));
}
}Definissons maintenant la classe principale Environment, qui propose plusieurs environnements et qui va s'occuper de visualiser notre grille et nos algorithmes de recherche.
Environment class
package environment;
import robot.Configuration2D;
import robot.Robot;
import io.jbotsim.core.Node;
import io.jbotsim.core.Topology;
import io.jbotsim.ui.JViewer;
import io.jbotsim.ui.painting.BackgroundPainter;
import io.jbotsim.ui.painting.UIComponent;
import java.awt.*;
import java.util.ArrayList;
public class Environment implements BackgroundPainter {
private Topology tp;
public static double resolution;
public static void main(String[] args) {
new Environment(3); //<---------------------change environment type (1,2 or 3) here
}
public Environment(int env){
tp = new Topology();
JViewer jv = new JViewer(tp);
jv.getJTopology().setDefaultBackgroundPainter(this);
tp.setNodeModel("robot", Robot.class);
tp.setNodeModel("target", Target.class);
tp.setNodeModel("fire", Fire.class);
resolution = GridNode.resolution;
switch (env) {
case 1 : //Open space
break;
case 2 : //Fire walls
addFireWalls();
break;
case 3 : //Random fire
addRandomFire(200);
break;
}
System.out.println("Place entity and target, then execute !");
}
private void addFireWalls() {
for (int x = tp.getWidth() / 4; x <= 3 * tp.getWidth() / 4; x += resolution) {
tp.addNode(x, tp.getHeight() / 4, new Fire());
}
for (int y = tp.getHeight() / 4; y <= 3 * tp.getHeight() / 4; y += resolution) {
tp.addNode(tp.getWidth() / 4, y);
tp.addNode(3 *tp.getWidth() / 4, y, new Fire());
}
for (int x = tp.getWidth() / 4; x <= tp.getWidth() / 2 - 50; x += resolution) {
tp.addNode(x,3 * tp.getHeight() / 4, new Fire());
}
for (int x = tp.getWidth() / 2 + 50; x <= 3 * tp.getWidth() / 4; x += resolution) {
tp.addNode(x,3 * tp.getHeight() / 4, new Fire());
}
}
private void addRandomFire(int nbFire) {
for (int i=0; i<nbFire; i++){
tp.addNode(-1,-1, new Fire());
}
}
@Override
public void paintBackground(UIComponent uiComponent, Topology topology) {
Graphics2D g2d = (Graphics2D) uiComponent.getComponent();
drawGrid(g2d, topology);
drawSearchAlgo(g2d, topology);
}
private void drawGrid(Graphics2D g2d, Topology topology) {
for (double i=resolution; i<topology.getWidth(); i+=resolution){
g2d.setColor(Color.lightGray);
g2d.drawLine((int)i, 0, (int)i, topology.getHeight());
}
for (double i=resolution; i<topology.getHeight(); i+=resolution){
g2d.setColor(Color.lightGray);
g2d.drawLine(0, (int)i, topology.getWidth(), (int)i);
}
}
private void drawSearchAlgo(Graphics2D g2d, Topology topology) {
for (Node n : topology.getNodes()) {
if (n instanceof Robot) {
try { //
Robot r = (Robot) n;
ArrayList<Configuration2D> l = r.getSearchAlgo().getSearchHistory();
for (Configuration2D p2 : l) {
if (p2.getParent() != null) {
Configuration2D p1 = p2.getParent();
g2d.setColor(Color.RED);
g2d.drawLine((int) p1.getX(), (int) p1.getY(),
(int) p2.getX(), (int) p2.getY());
}
}
//draws trajectory when found
ArrayList<Configuration2D> trajectory = r.getTrajectory();
if (!trajectory.isEmpty()){
for (int i=1; i<trajectory.size(); i++){
Configuration2D p1 = trajectory.get(i - 1);
Configuration2D p2 = trajectory.get(i);
g2d.setColor(Color.GREEN);
g2d.drawLine((int) p1.getX(), (int) p1.getY(),
(int) p2.getX(), (int) p2.getY());
}
}
} catch (Exception e) { } //nothing
}
}
}
}Évidemment, il manque le plus important : une entité autonome. Voilà la classe Robot.
Robot class
package robot;
import robot.algorithms.*;
import io.jbotsim.ui.icons.Icons;
import environment.GridNode;
import java.util.ArrayList;
public class Robot extends GridNode {
private ArrayList<Configuration2D> trajectory;
private int trajectoryIterator;
private double speed;
private SearchAlgorithm searchAlgo;
public Robot(){
setIcon(Icons.ROBOT);
setIconSize((int)(getIconSize()*1.5));
trajectory = new ArrayList();
trajectoryIterator = 0;
speed = 2.5;
}
@Override
public void onStart() {
super.onStart();
searchAlgo = new BFS(this); //<--------------------------change the search algorithm
searchAlgo.onStart();
}
@Override
public void onClock() {
super.onClock();
if(trajectory.isEmpty()) {
searchAlgo.onClock();
} else {
followTrajectory();
}
}
private void followTrajectory() {
if (trajectoryIterator < trajectory.size()) {
Configuration2D next = trajectory.get(trajectoryIterator);
setDirection(next);
move(speed);
if (distance(next) < speed){
trajectoryIterator++;
}
}
}
public ArrayList<Configuration2D> getTrajectory(){
return trajectory;
}
public void setTrajectory(ArrayList<Configuration2D> list){
trajectory = list;
}
public SearchAlgorithm getSearchAlgo(){
return searchAlgo;
}
}Il ne manque plus que l'espace des configurations du robot, ainsi qu'un algorithme pour chercher dans cet espace.
Pour construire l'espace des configurations du robot, nous supposons que :
- Le robot peut se déplacer dans quatre directions, notamment sud, nord, est et ouest.
- Le robot se déplace de 10 chaque unité de temps, dans une des directions.
- Il existe un endroit $(t_x, t_y)$ accessible au robot, tel que la cible est considérée visitée si le robot a la configuration $(t_x, t_y)$.
- Le robot se trouve initialement sur $(r_x, r_y)$, avec $r_x, r_y$ des multiples de 10.
Ces suppositions vont main en main avec le fait que l'on place nos noeuds automatiquement sur une grille de résolution 10.
L'espace des configurations se construit maintenant autour du sommet représentant la configuration de départ, donc $(r_x, r_y)$. Après 1 unité de temps, le robot pourrait se trouver à quatre positions distinctes, notamment $(r_x + 10, r_y)$, $(r_x, r_y + 10)$, $(r_x - 10, r_y)$ ou $(r_x, r_y - 10)$. On crée alors quatre nouvaux sommets dans l'espace des configurations représentant ces quatre positions, et on crée des arcs du sommet de départ vers chacun de ces nouveaux sommets. Ce processus se répète maintenant pour les nouveaux sommets. Prenons le sommet représentant la configuration $(r_x + 10, r_y)$. Les prochaines configurations possibles à partir de celle-ci sont $(r_x + 20, r_y)$, $(r_x, r_y)$, $(r_x + 10, r_y + 10)$ et $(r_x + 10, r_y - 10)$. On ne rajoute cette fois-ci que trois nouveaux sommets car la configuration $(r_x, r_y)$ est déjà présente dans l'espace des configurations. On crée des arcs de $(r_x + 10, r_y)$ aux 4 sommets. En continuant ce processus, on observe bien que l'espace créé correspond en fait à $(10x, 10y)$, pour tout $x$ et $y$ entiers, avec des arcs de toute configuration $(x, y)$ vers $(x', y')$ si $|x' - x| + |y' - y| \leq 10$.
Remarque : Il est important de faire des suppositions simples, mais suffisantes. Par exemple, on aurait pu faire la supposition que le robot puisse bouger dans la direction ouest, mais elle n'est pas suffisante si jamais la cible se trouve au nord du départ. En revanche, la supposition que le robot puisse bouger dans les directions nord, sud, est, ouest, nord-est, nord-ouest, sud-est et sud-ouest est suffisante, mais risque de créer beaucoup plus de sommets et d'arcs dans l'espace des configurations, compliquant rapidement la recherche de chemin. La supposition que le robot puisse se déplacer de au plus 10 centimètres, crée une infinité de sommets et d'arcs, compliquant encore plus la recherche de chemin !
Dans JBotSim, nous avons décidé de créer l'espace des configurations pendant que l'on cherche la cible, au lieu de le créer en entier avant de commencer la recherche. Ceci est pour éviter de créer d'abord un espace gigantesque (voire infini), avec de nombreux sommets et arcs, pour finalement parcourir que quelques sommets/arcs avant de trouver la cible. Nous encodons l'espace des configurations en utilisant la classe suivante, qui va représenter un sommet $(x, y)$ de l'espace. Chaque sommet se rappelle de son sommet parent, ce qui va nous être utile pour remonter le chemin une fois la cible trouvée. On a décidé également d'étendre de la classe Point de JBotSim, sachant que chaque configuration du robot correspond à un point 2D (une position, si vous voulez) avec un parent.
Configuration2D class
package robot;
import io.jbotsim.core.Point;
public class Configuration2D extends Point {
private Configuration2D parent;
public Configuration2D(double x, double y, Configuration2D parent){
super(x, y);
this.parent = parent;
}
public Configuration2D getParent() {
return parent;
}
}Regardons maintenant comment chercher un chemin dans l'espace des configurations. Commençons par créer une classe abstraite pour les algorithmes de recherche de chemin, pour éviter de dupliquer du code dans nos différents algorithmes.
SearchAlgorithm class
package robot.algorithms;
import environment.Fire;
import environment.Target;
import io.jbotsim.core.Node;
import io.jbotsim.core.Topology;
import robot.Configuration2D;
import robot.Robot;
import java.util.ArrayList;
import java.util.Collections;
public abstract class SearchAlgorithm {
protected Configuration2D start;
protected Configuration2D target = new Configuration2D(0,0, null); //temporary setting
protected ArrayList<Configuration2D> searchHistory;
protected Robot r;
public SearchAlgorithm(Robot r){
this.r = r;
searchHistory = new ArrayList();
}
public void onStart(){
start = new Configuration2D(r.getX(), r.getY(), null);
for (Node n : r.getTopology().getNodes()){
if (n instanceof Target){
((Target)n).reposition();
target = new Configuration2D(n.getX(), n.getY(), null);
}
}
}
public abstract void onClock();
protected boolean valid(Configuration2D current) {
// Testing if passed through fire
Topology tp = r.getTopology();
Configuration2D parent = current.getParent();
if (parent != null) {
for (Node fire : tp.getNodes()) {
if (fire instanceof Fire){
if(fire.distance(current) <= Fire.safetyDistance){
return false;
}
}
}
}
//Testing if out of bounds
double x = current.getX();
double y = current.getY();
if (x <= 0 || y <= 0 || x >= tp.getWidth() || y >= tp.getHeight()){
return false;
}
return true; //valid
}
protected boolean foundTarget(Configuration2D current) {
if (current.getX() == target.getX() && current.getY() == target.getY()){
return true;
}
return false;
}
protected void retraceTrajectory(Configuration2D p) {
ArrayList<Configuration2D> result = new ArrayList<>();
result.add(p);
while(p.getParent() != null){
p = p.getParent();
result.add(p);
}
Collections.reverse(result);
r.setTrajectory(result);
}
public ArrayList<Configuration2D> getSearchHistory(){
return searchHistory;
}
}Premier algorithme est l'algorithme de parcours en largeur. Nous commençons au sommet de départ et à chaque étape nous allons vérifier le sommet actuel, puis stocker dans une structure de données les sommets adjacents, pour pouvoir les récupérer dans les étapes suivantes. On utilise une file comme structure de données. Pour rappel, une file a le comportement premier entré, premier sorti. Ceci va nous permettre de d'abord explorer proche du sommet du départ dans l'espace des configurations, ce qui va nous assurer l'optimalité du chemin retourné.
BFS class
package robot.algorithms;
import robot.Configuration2D;
import robot.Robot;
import java.util.LinkedList;
import java.util.Queue;
public class BFS extends SearchAlgorithm {
Queue<Configuration2D> queue = new LinkedList();
public BFS(Robot r) {
super(r);
}
@Override
public void onStart() {
super.onStart();
Configuration2D start = new Configuration2D(r.getX(), r.getY(), null);
queue.add(start);
}
@Override
public void onClock() {
Configuration2D current = queue.remove();
if (!valid(current)){
//nothing
return;
}
if (!foundTarget(current)) {
double resolution = r.getResolution();
Configuration2D child1 = new Configuration2D(current.getX() + resolution,
current.getY(),
current);
Configuration2D child2 = new Configuration2D(current.getX() - resolution,
current.getY(),
current);
Configuration2D child3 = new Configuration2D(current.getX(),
current.getY() + resolution,
current);
Configuration2D child4 = new Configuration2D(current.getX(),
current.getY() - resolution,
current);
if (!searchHistory.contains(child1) && !queue.contains(child1)) {
queue.add(child1);
}
if (!searchHistory.contains(child2) && !queue.contains(child2)) {
queue.add(child2);
}
if (!searchHistory.contains(child3) && !queue.contains(child3)) {
queue.add(child3);
}
if (!searchHistory.contains(child4) && !queue.contains(child4)) {
queue.add(child4);
}
searchHistory.add(current);
return;
}
if (r.getTrajectory().isEmpty()) {
retraceTrajectory(current);
}
}
}Vous ne devriez plus avoir des erreurs dans le code (hors peut-être des erreurs de paquet, que vous saviez résoudre avec les touches magiques). Exécutez donc la classe Environment et placez votre cible et le robot dans la fenêtre JBotSim, puis démarrez. N'hésitez pas à monter la vitesse du système JBotSim. Vous pouvez changer d'environnement (1, 2 ou 3) dans la classe respective, pour être sûr d'avoir bien compris l'algorithme qui va chercher autour du robot, dans toutes les directions.
Remarque : L'algorithme de Dijkstra, dans des graphes sans poids sur les arêtes, a le même comportement que cet algorithme de parcours en largeur. En plus, en traitement d'image, cet algorithme est connu sous nom de Grassfire (exécutez dans l'environnement 1 et vous verrez pourquoi).
Changeons d'algorithme. L'algorithme A étoile est similaire à l'algorithme précédent. Nous allons utiliser une autre structure de données qu'une file. Nous utilisons dans A étoile une file de priorité. Il est important de noter que les files de priorités n'ont rien avoir avec les files, dans le sens où premier entré, premier sorti ne s'applique pas du tout pour les files de priorité. En effet, dans les files de priorité, nous allons stocker des sommets ayant tous une priorité. Cette priorité est alors comparée aux priorités des sommets déjà présents dans la file, et le sommet est inséré dans la file par ordre ascendant de priorité. Le comportement peut être décrit simplement comme meilleur sorti en premier avec le meilleur ayant la plus basse priorité, ce qui guiderait donc la recherche dans une direction promettante.
Dans notre cas, la priorité d'un sommet de l'espace des configurations va correspondre au chemin le plus court passant par ce sommet. Bien entendu, nous ne connaissons pas le chemin le plus court passant par ce sommet, car c'est bien pour obtenir le chemin le plus court que nous codons ces algorithmes ! Alors nous allons utiliser une fonction d'estimation du chemin restant à calculer à partir du sommet. Bref, la priorité d'un sommet se calcule : priorité = longueur du chemin depuis départ + estimation du chemin restant jusqu'à la cible. Nous utiliserons comme fonction d'estimation la distance euclidienne entre le sommet et la cible, divisée par la distance que le robot parcourt en une unité de temps.
AStar class
package robot.algorithms;
import environment.Target;
import io.jbotsim.core.Node;
import robot.Configuration2D;
import robot.Robot;
import java.util.PriorityQueue;
public class AStar extends SearchAlgorithm{
private PriorityQueue<Configuration2D> prioQueue;
public AStar(Robot r) {
super(r);
}
@Override
public void onStart() {
super.onStart();
prioQueue = new PriorityQueue<>();
Configuration2D start = new Configuration2D(r.getX(), r.getY(), null);
prioQueue.add(start);
}
@Override
public void onClock() {
Configuration2D current = prioQueue.remove();
if (!valid(current)){
//nothing
return;
}
if (!foundTarget(current)) {
double resolution = r.getResolution();
Configuration2D child1 = new Configuration2D(current.getX() + resolution,
current.getY(),
current);
Configuration2D child2 = new Configuration2D(current.getX() - resolution,
current.getY(),
current);
Configuration2D child3 = new Configuration2D(current.getX(),
current.getY() + resolution,
current);
Configuration2D child4 = new Configuration2D(current.getX(),
current.getY() - resolution,
current);
if (!searchHistory.contains(child1) && !prioQueue.contains(child1)) {
computePriority(r, child1);
prioQueue.add(child1);
}
if (!searchHistory.contains(child2) && !prioQueue.contains(child2)) {
computePriority(r, child2);
prioQueue.add(child2);
}
if (!searchHistory.contains(child3) && !prioQueue.contains(child3)) {
computePriority(r, child3);
prioQueue.add(child3);
}
if (!searchHistory.contains(child4) && !prioQueue.contains(child4)) {
computePriority(r, child4);
prioQueue.add(child4);
}
searchHistory.add(current);
return;
}
if (r.getTrajectory().isEmpty()) {
retraceTrajectory(current);
}
}
private void computePriority(Robot d, Configuration2D p) { //simulate best case scenario
for (Node target : d.getTopology().getNodes()){
if (target instanceof Target){
double est = p.distance(target.getLocation()) / d.getResolution();
p.setPriority(p.getLayer() + est);
}
}
}
}Ce code ne va pas apprécier le fait que les sommets de l'espace de configuration Configuration2D ne sont pas Comparable, car la file de priorité ne va pas pouvoir comparer les sommets entre eux. Rendons les sommets donc Comparable, en précisant qu'il faudrait utiliser leur paramètre priority pour pouvoir se comparer entre eux :
Configuration2D class
package robot;
import io.jbotsim.core.Point;
public class Configuration2D extends Point implements Comparable {
private Configuration2D parent;
private double layer;
private Double priority;
public Configuration2D(double x, double y, Configuration2D parent){
super(x, y);
this.parent = parent;
if (parent == null) {
layer = 0;
} else {
layer = parent.layer + 1;
}
}
public Configuration2D getParent() {
return parent;
}
public double getLayer(){
return layer;
}
public double getPriority(){
return priority;
}
public void setPriority(double prio){
priority = prio;
}
@Override
public int compareTo(Object o) {
Configuration2D p = (Configuration2D) o;
return priority.compareTo(p.getPriority());
}
}Changez l'algorithme que le robot utilise dans sa classe, puis relancez Environment. Dans l'environnement 1, on voit très bien que la recherche de chemin va rapidement chercher dans la bonne direction. Dans l'environnement 2 (voir image ci-dessous), on peut observer que l'algorithme A étoile peut être "piégé" d'aller chercher directement proche de la cible, qui est entourée de murs. Néanmoins, en général, cet algorithme finit plus rapidement que l'algorithme de parcours en largeur !
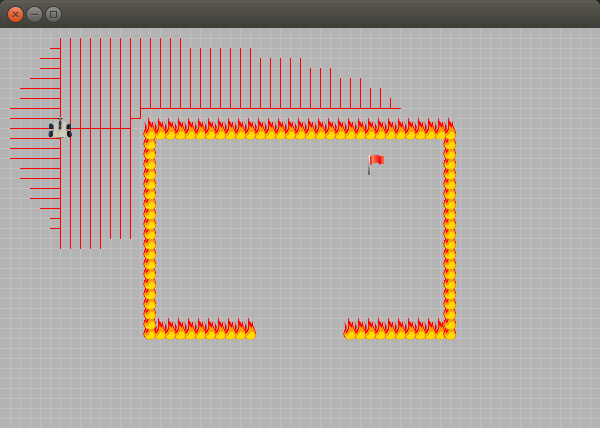
Exemple d'une instance où l'algorithme A étoile va chercher d'abord dans une mauvaise direction, car il ne tient pas compte des obstacles.
A étoile bidirectionnel
Ce dernier algorithme est basé sur une modification de l'algorithme A étoile . Cette modification n'est pas propre à A étoile , dans le sens où on aurait pû l'appliquer sur l'algorithme de parcours en largeur également. La modification consiste à chercher en même temps dans les deux sens. C'est à dire, effectuer un algorithme A étoile non seulement à partir du sommet du départ, mais également à partir du sommet correspondant à la cible. Quand les deux algorithmes A étoile se "touchent" sur un même sommet, les deux bouts de chemin sont collés et retournés comme un seul chemin résultant.
Nous choisissons d'encoder cet algorithme tel que, à chaque onClock(), une étape se passe pour l'algorithme A étoile partant du départ, ainsi qu'une étape pour l'algorithme A étoile partant de la cible.
BiAStar class
package robot.algorithms;
import robot.Configuration2D;
import robot.Robot;
import java.util.ArrayList;
import java.util.Collections;
import java.util.PriorityQueue;
public class BiAStar extends SearchAlgorithm {
private Configuration2D start;
private PriorityQueue<Configuration2D> prioQueue1;
private PriorityQueue<Configuration2D> prioQueue2;
private ArrayList<Configuration2D> searchHistory2;
public BiAStar(Robot r) {
super(r);
}
public void onStart() {
super.onStart();
prioQueue1 = new PriorityQueue<>();
prioQueue2 = new PriorityQueue<>();
searchHistory2 = new ArrayList<>();
start = new Configuration2D(r.getX(), r.getY(), null);
prioQueue1.add(start);
prioQueue2.add(target);
}
public void onClock() {
Configuration2D current = prioQueue1.remove();
Configuration2D current2 = prioQueue2.remove();
Configuration2D intersection = new Configuration2D(0,0, null);
boolean found = false;
if (!valid(current)){
//nothing
}
else {
if (!prioQueue2.contains(current)) {
double resolution = r.getResolution();
Configuration2D child1 = new Configuration2D(current.getX() + resolution,
current.getY(),
current);
Configuration2D child2 = new Configuration2D(current.getX() - resolution,
current.getY(),
current);
Configuration2D child3 = new Configuration2D(current.getX(),
current.getY() + resolution,
current);
Configuration2D child4 = new Configuration2D(current.getX(),
current.getY() - resolution,
current);
if (!searchHistory.contains(child1) && !prioQueue1.contains(child1)) {
computePriority(child1, target);
prioQueue1.add(child1);
}
if (!searchHistory.contains(child2) && !prioQueue1.contains(child2)) {
computePriority(child2, target);
prioQueue1.add(child2);
}
if (!searchHistory.contains(child3) && !prioQueue1.contains(child3)) {
computePriority(child3, target);
prioQueue1.add(child3);
}
if (!searchHistory.contains(child4) && !prioQueue1.contains(child4)) {
computePriority(child4, target);
prioQueue1.add(child4);
}
searchHistory.add(current);
} else {
found = true;
intersection = current;
searchHistory.add(current);
}
}
if (!found) {
if (!valid(current2)) {
//nothing
return;
} else {
if (!prioQueue1.contains(current2)) {
double resolution = r.getResolution();
Configuration2D child1 = new Configuration2D(current2.getX() + resolution,
current2.getY(),
current2);
Configuration2D child2 = new Configuration2D(current2.getX() - resolution,
current2.getY(),
current2);
Configuration2D child3 = new Configuration2D(current2.getX(),
current2.getY() + resolution,
current2);
Configuration2D child4 = new Configuration2D(current2.getX(),
current2.getY() - resolution,
current2);
if (!searchHistory2.contains(child1) && !prioQueue2.contains(child1)) {
computePriority(child1, start);
prioQueue2.add(child1);
}
if (!searchHistory2.contains(child2) && !prioQueue2.contains(child2)) {
computePriority(child2, start);
prioQueue2.add(child2);
}
if (!searchHistory2.contains(child3) && !prioQueue2.contains(child3)) {
computePriority(child3, start);
prioQueue2.add(child3);
}
if (!searchHistory2.contains(child4) && !prioQueue2.contains(child4)) {
computePriority(child4, start);
prioQueue2.add(child4);
}
searchHistory2.add(current2);
} else {
found = true;
intersection = current2;
searchHistory2.add(current2);
}
}
}
if (found && r.getTrajectory().isEmpty()) {
retraceTrajectory(intersection);
}
}
private void computePriority(Configuration2D p, Configuration2D dest) { //simulate best case scenario
double est = p.distance(dest) / r.getResolution();
p.setPriority(p.getLayer() + est);
}
}Pour retrouver le bon chemin, il va également falloir @Override (dans la classe BiAStar) les méthodes retraceTrajectory de la classe SearchAlgorithm, comme il y a maintenant deux bouts de chemins à coller ensemble. Pour bien visualiser l'algorithme sous JBotSim, il faut également @Override getSearchHistory, comme on a deux historiques de recherche maintenant. Une façon de faire est la suivante :
@Override
protected void retraceTrajectory(Configuration2D p) {
ArrayList<Configuration2D> result = new ArrayList<>();
Configuration2D aux = new Configuration2D(p.getX(), p.getY(), p.getParent());
result.add(aux);
while(aux.getParent() != null){
aux = aux.getParent();
result.add(aux);
}
Collections.reverse(result);
if (aux.equals(start)){
for (Configuration2D p2 : prioQueue2) {
if (p2.equals(p)) {
while (p2.getParent() != null) {
p2 = p2.getParent();
result.add(p2);
}
break;
}
}
} else {
for (Configuration2D p2 : prioQueue1) {
if (p2.equals(p)) {
while (p2.getParent() != null) {
p2 = p2.getParent();
result.add(p2);
}
break;
}
}
Collections.reverse(result);
}
r.setTrajectory(result);
}
@Override
public ArrayList<Configuration2D> getSearchHistory() {
ArrayList<Configuration2D> result = new ArrayList<>(searchHistory);
result.addAll(searchHistory2);
return result;
}Exercices
Q1. Créez l'algorithme parcours en profondeur (DFS), dans le paquet robot.algorithms, qui a le même fonctionnement que l'algorithme parcours en largeur (BFS), sauf que l'on utilise une pile comme structure de données, au lieu d'une file. Changez l'algorithme du robot, puis exécutez.
Q2. Vous remarquerez rapidement la différence de qualité entre les deux algorithmes. L'algorithme de parcours en profondeur ne retourne (en général) pas un plus court chemin, tandis que l'algorithme parcours en largeur si. Cet algorithme n'a donc pas sa place pour par exemple une application GPS. Néanmoins, l'algorithme peut être utile dans les jeux vidéos, comme par exemple pour créer un bot un peu bête ou imprévisible, ou dans notre cas, un robot défectueux. Adaptez l'algorithme pour que le chemin retourné ne soit pas toujours le même chemin, pour créer par exemple un bot encore plus imprévisible. Ceci peut se faire en insérant en ordre aléatoire les quatre fils créés dans la pile. Testez plusieurs fois, pour vous assurer que le robot prend bien un chemin différent à chaque fois, et d'une longueur différente à chaque fois également.
Remarque : De la même façon, nous pouvons faire en sorte que l'algorithme parcours en largeur nous retourne un chemin différent à chaque fois, en supposant que plusieurs chemins optimaux existent.
Q3. Dans le pire cas, combien de configurations estimez-vous qu'il puisse y avoir dans notre espace de taille $600 \times 400$ ? rappellez-vous que le robot puisse prendre que des états de la forme $(10x, 10y)$. En général, combien d'états ceci fait dans un espace de taille $n \times n$ ?
Q4. La distance manhattan s'agit de la distance entre deux points mesurée le long des axes aux angles droits. Par exemple, la distance euclidienne entre (0,0) et (1,1) est $\sqrt{|1-0|^2 + |1-0|^2} = 1.41$, tandis que la distance manhattan entre ces points est $|1-0| + |1-0| = 2$.
- Quelle est la distance euclidienne entre $(0,0)$ et $(10,20)$ ? Et sa distance manhattan ?
- Même question, mais pour les points $(10, 15)$ et $(22,3)$ ?
Q5. Dans l'algorithme A étoile , on utilise une fonction d'estimation basée sur la distance euclidienne. Changez la pour une meilleure fonction d'estimation basée sur la distance manhattan. N'oubliez pas de garder la division par r.getResolution(), qui est de 10 (car le robot bouge de 10 à chaque unité de temps).
Remarque : Une bonne fonction d'estimation dans A étoile doit se rapprocher le plus possible par le bas au vrai coût. En d'autres mots, elle ne doit jamais sur-estimer un coût. Ceci est pour garantir l'optimalité du chemin retourné.
Q6 (bonus). Créez l'algorithme parcours en largeur bidirectionnelle.
Q7 (bonus). L'algorithme A étoile bidirectionnelle, tel qu'on l'a donné, ne garantie pas l'optimalité du chemin retourné. En effet, il est possible de trouver un meilleur chemin si il existe encore des sommets dans les deux files de priorités, qui estiment faire mieux que le chemin déjà trouvé ! Ceci peut se corriger de deux façons, soit en vérifiant si il ne reste plus de sommets dans les files estimant faire mieux que le coût du chemin déjà trouvé, soit par l'utilisation d'une seule file pour les deux algorithmes A étoile . Adaptez l'algorithme A étoile bidirectionnelle donné, pour qu'il retourne un chemin optimale.