STGen: A generator of simple and proper temporal graphs
(Last updated: July 15, 2024.)
Table of content
Overview | How to use STGen | Parallel iterators | The TGraph class | How to cite STGen
Overview of STGen
A temporal graph is simple if every edge has a single time label. It is proper if two edges incident to a same vertex have different time labels. If a graph is both proper and simple, we call it happy.
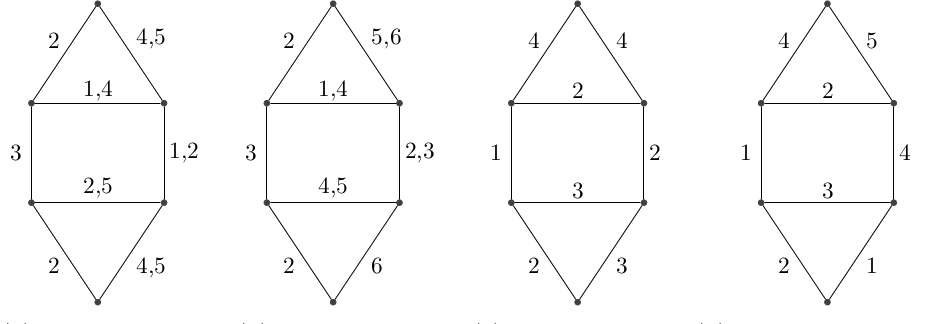
Fig. 1. From left to right: Non-proper and non-simple; Proper and non-simple; Simple and non-proper; Simple and proper (happy).
STGen enumerates all happy temporal graphs, up to isomorphism. The notion of isomorphism here also considers as identical all the graphs whose local ordering of the edges is the same. For example, in Fig. 2, the left and middle graphs are equivalent in the sense that their temporal paths are in bijection.
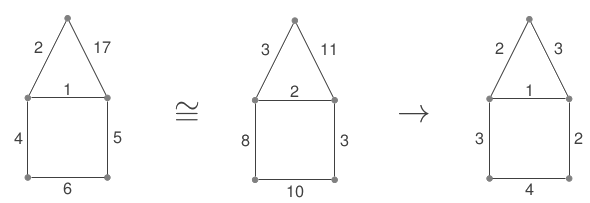
Fig. 2. Canonical representatives of happy temporal graphs.
The graph on the right is, among all the graphs in the same equivalence class, the one that uses the lowest possible time labels. Up to standard (i.e. static) isomorphism of labeled graphs, this graph is unique, and can thus be seen as the canonical representative of this class of happy graphs.
STGen actually generates all (and only) such canonical representatives. For a fixed number of vertices n, these graphs are in finite number and can be enumerated. Unfortunately, their number still grows essentially like \({n \choose 2}!\). One may hope for manipulating graphs of order up to 7 (or perhaps 8, if complete enumeration is not required), but enumerating significant fractions of larger graphs seems out of reach.
To get an idea of the growth, here are the numbers of representatives on 3, 4, 5, 6, and 7 vertices:
| n | # Happy graphs (representatives) |
|---|---|
| 3 | 4 |
| 4 | 62 |
| 5 | 15378 |
| 6 | 89769096 |
| 7 | 13725757879376 |
Number of temporal cliques (complete happy graphs on n vertices):
| n | # Happy cliques (representatives) |
|---|---|
| 3 | 1 |
| 4 | 20 |
| 5 | 4524 |
| 6 | 23218501 |
| 7 | 3106952711040 |
The numbers for n=8 are unknown. Still, some properties on happy graphs of order 8 can be tested exhaustively, thanks to a branch-cutting mechanism in the generation (see below).
The generation tree
STGen relies on a generation tree, each node of which is a happy graph that contains its parent as a proper subgraph. The root of the tree is the empty graph on n vertices. The set of successors of a graph corresponds to all the possible ways to add the next time label to this graph, up to isomorphism (see Figure 2), while remaining a valid representative – among other things, this implies that edge can receive label t only if it is adjacent to an edge having label t-1 (contiguity lemma).
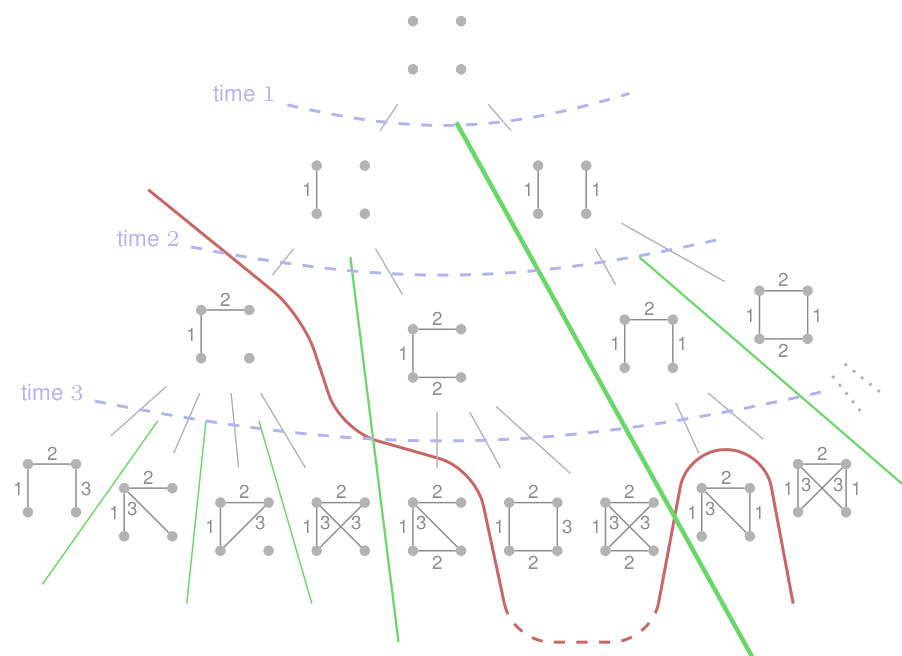
Fig. 3. (Top of) the generation tree for n=4.
This monotonous assignment of time labels is what guarantees that isomorphism types are separated forever down the tree (green separation lines on the Figure). Indeed, if two graphs are different at a certain stage, then their successors will always remain separated due to the already assigned labels.
Interestingly, the same property also guarantees that once a graph becomes rigid, i.e., it has no non-trivial automorphisms, then none of its successors will be symmetric again. Thus, there is an irrevocable boundary in the generation tree between symmetric graphs (in the top of the tree) and rigid graphs (below the boundary) – see the red line in Figure 3.
In both cases, each successor is characterized by a unique set of independent new edges (a matching in the complement graph) to which the next label is assigned. (Why a matching? because happy graphs are proper!) When the graph is symmetric, STGen ensures that no two such matchings are equivalent up to automorphisms (in the parent graph), which guarantees unicity among the successors. For rigid graphs, this property is ensured without caring about automorphisms, making the generation very fast.
How to use STGen
Installation
You can download STGen as a single zip file or clone it from its github repository. The folder contains a minimal working example (in the main.cpp file) described next. You need to have a reasonably recent C++ compiler (e.g. at least g++-11). If you want to use the parallel iterators, you also need to have a TBB implementation installed in your system (e.g. sudo apt install libtbb12 or sudo apt install libtbb2 depending on your version of C++, as well as sudo apt install libtbb-dev). The suggested compilation line, also present in the Makefile, is:
g++ -O3 main.cpp -o main -ltbb -march=native
The last two arguments are optional: -ltbb if you want STGen to use parallelism, -march=native for better performance (but less portability).
Basic examples
Using STGen is pretty straightforward. You must declare a TGraphIterator, giving as template parameter the desired number of vertices and as argument a user-defined function to which STGen will pass every generated graph.
Here is a complete example that simply counts the number of happy graphs on 6 vertices:
#include "stgen/stgen.h"
const int N = 6;
using namespace stgen;
bool count_all(const TGraph<N>& g, int64_t& nb){
nb++; // count this graph
return true; // generate the successors
};
int main(){
TGraphIterator<N> iter(count_all);
int64_t nb = iter.execute();
std::cout << nb << std::endl;
}
$ time ./main
89769096
real 0m2,647s
In this case, we implemented a basic function called count_all() (it could have any name) that consists of counting every graph and doing nothing else. More generally, the arguments of this function are the graph being visited (const TGraph<N>& g) and a number (int64_t& nb) that can be incremented or not depending on what we want to count (you can ignore it, if you don’t want to count anything). Your return value must indicate to STGen whether it should generate the successors of that graph (true) or cut this branch of the tree (false). Cutting branches is crucial if you manipulate happy graphs on more than 6 vertices.
Here is another example that counts all happy cliques:
#include "stgen/stgen.h"
const int N = 6;
const int M = (N*(N-1))/2;
using namespace stgen;
bool count_cliques(const TGraph<N>& g, int64_t& nb){
if (g.nb_edges == M){
nb++;
}
return true;
};
int main(){
TGraphIterator<N> iter(count_cliques);
int64_t nb = iter.execute();
std::cout << nb << std::endl;
}
$ time ./main
23218501
real 0m2,541s
Let’s say we now want all the cliques whose lifetime (i.e. maximum label) is at most 8. The corresponding function could be as follows:
bool count_cliques_lifetime_at_most_8(const TGraph<N>& g, int64_t& nb){
if (g.lifetime > 8){
return false; // cut the subtree
} else {
if (g.nb_edges == M){
nb++; // or do anything else here on those cliques
}
return true;
}
};
int main(){
TGraphIterator<N> iter(count_cliques_lifetime_at_most_8);
int64_t nb = iter.execute();
std::cout << nb << std::endl;
}
$ time ./main
134764
real 0m0,533s
As we can see here, the generation is faster, because all the graphs whose lifetime exceed 8 have been cut off (together with their subtrees).
Parallel iterators
STGen offers two parallel iterators, depending on your needs: TGraphParIterator (basic) and TGraphBatchIterator (advanced). Both are similar in terms of performance, their differ only in their simplicity (versus scaling abilities). The basic version is appropriate if you are targetting graphs of up to 7 vertices and intend to run the experiment in one shot on a single computer. In contrast, the batch iterator allows you to split the work into several batches to be executed independently on several computers (possibly at different times), which is often necessary if you target graphs of 8 or more vertices. It may also be more appropriate for some experiments on 7 vertices, if your computation is heavy and/or does not cut many branches.
The TGraphParIterator iterator
This iterator is used exactly in the same way as the standard TGraphIterator. Simply replace the type in the declaration. For example,
int main(){
TGraphParIterator<N> iter(count_cliques_lifetime_at_most_8);
int64_t nb = iter.execute();
std::cout << nb << std::endl;
}
$ time ./main
134764
real 0m0,150s
Using this iterator gives a much faster execution (here, on my 6-core computer). You need not worry about race conditions for the function parameters. In particular, the nb variable is local to each subtree and never shared among threads.
You probably do not need to understand how this iterator works internally. But since you are curious: First, the top of the tree (part above the red line in Figure 3) is processed on a single cpu, storing the boundary graphs (first graphs to be rigid) in a collection. Then, the subtrees of each of these graphs are processed in parallel and independently, exploiting whichever cpu is available on your computer (summing up the resulting nb variables in a map reduce fashion). Note that, up to 7 vertices, the top of the tree is computed almost instantaneously, but this is not the case for 8 vertices.
The TGraphBatchIterator iterator
An experiment on graphs of 8 or more vertices is likely to be impractical on a single computer, even if it has many cores. The batch iterator makes it possible to split the work into a collection of batches, each of which can be executed independently and at different times.
Technically, the work is split according to a two-level hierarchy. First, a small subset of the top of the tree is generated using a single thread. Each graph along the resulting boundary (this time, higher than the red line in Figure 3) is seen as a separate batch, with a unique batch number. Every batch can then be executed independently, by specifying the batch number. The execution of an individual batch follows the same mechanism as the basic parallel iterator: the top of the batch is executed on a single thread until some depth is reached, then the graphs along this second boundary (and their subtrees) are explored in parallel.
This behavior is mostly transparent to the user. What you need to know is that the number of batches is automatically determined by STGen (you do not control it). It is computed upon creation of the iterator and you can access it as follows:
TGraphBatchIterator<N> iter(my_function);
int nb_batches = iter.number_of_batches();
You can then execute a given batch as follows:
int64_t nb = iter.execute(BATCH_NUM);
where BATCH_NUM is the batch that you want to execute (between 0 and nb_batches-1).
It is your job to sum up the resulting numbers if you want to count something over the entire experiment. For the sake of example, here is a program that executes all the batches on a single computer, it is unlikely that you want to use the batch iterator in this way (unless you want to monitor the progress and/or be able to resume execution after an interruption):
int main(){
TGraphBatchIterator<N> iter(my_function);
int nb_batches = iter.number_of_batches();
int64_t nb = 0;
for (int i=0; i < nb_batches; i++){
std::cout << "processing batch " << i << std::endl;
nb += iter.execute(i);
}
std::cout << nb << std::endl;
}
Here is the outcome for N=6 with the count_all() function:
$ ./main
processing batch 0
processing batch 1
...
processing batch 2243
processing batch 2244
89769096
So, here, the work was split into 2245 batches. Note that the very top of the tree (the part higher than the batches) may itself result in some increments of the nb variable in your function. For convenience, this quantity is added to the result of the first batch, so that the sum of all the batches corresponds indeed to the entire tree.
The TGraph class
STGen is shipped with a default type of temporal graph, which is very basic. It is given in the tgraph.hpp file, and provides the following members:
template<int N, int M=(N*(N-1)/2)>
struct TGraph {
std::bitset<M> edges;
std::bitset<M> max_edges;
TEdge<N> tedges[M];
int nb_edges;
int lifetime;
...
}
For performance reasons, this class is templated with parameters N and M, where N is the number of vertices that the user specifies when an iterator is created (as in the examples above). The value of M is automatically instantiated to \({N \choose 2}\), the maximum number of edges in a graph of that size. The edges member is a bitset that indicates which edge is present in the footprint (edges without time information), ordered lexicographically by the corresponding pairs of vertices. The max_edges member is a bitset that indicates which of these edges currently hold maximum time labels, ordered similarly. These two members are required for generation, you should not touch them. The other three members are provided for your manipulations in the user function: tedges is an array containing M triplets (u,v,t). Among them, only the first nb_edges entries are meaningful. Here, the ordering is done according to time (not lexicography). Thus, if you iterate over the first nb_edges entries of the tedges array, concretely, you are iterating over all the time edges of the temporal graph in chronological order. Finally, the maximum time label among these edges is stored in the lifetime member.
Apart from its constructors, this class only provides a single member function is_tc(), which allows you to test if the given graph is temporally connected, and a function that overrides the << operator for printing the edges using cout << my_graph. The code of the is_tc() function is as follows:
bool is_tc() const{
bitset<N> predecessors[N];
for (int i=0; i<N; i++) {
predecessors[i].set(i);
}
for (int i=0; i<nb_edges; i++){
TEdge<N> e = tedges[i];
predecessors[e.u] |= predecessors[e.v];
predecessors[e.v] = predecessors[e.u];
}
for (int i=0; i<N; i++){
if (! predecessors[i].all()){
return false;
}
}
return true;
}
Using your own TGraph class
It is perfectly possible (and even encouraged) to enrich the TGraph class by adding further member variables and functions to this class according to your needs. So long as you do not touch the edges and max_edges member variables (nor their processing in the constructors), STGen will continue to work just fine and deliver to the user function your custom type of graph. If you want to do so, simply replace the tgraph.hpp file in the directory with your own version, whose type must also be called TGraph – this is a bit artisanal, but simple.
In way of an example, there is another file in the directory called tgraph_min, which corresponds to the bare minimum that STGen needs. If your goal is only to count the number of happy graphs (or happy cliques), this class is sufficient and will result in significant performance gain compared to the default TGraph version presented above (mostly, because the tedges array is not required for generation). Note that you can still test if a graph g is a clique using g.edges.all() instead of g.nb_edges == M in the above examples, or more generally, count the number of edges with g.edges.count() (just a bit slower).
Other versions of the TGraph class exist, which are not public yet. These classes will be made public later, together with a blog post dedicated to specific experiments.
How to cite STGen
If you are using STGen in your experiments, please cite it as follows:
@misc{stgen,
author = {Arnaud Casteigts},
title = {Efficient generation of simple and proper temporal graphs up to isomorphism},
note = {\texttt{https://arnaudcasteigts.net/blog/stgen.html}},
year = 2024,
}
(replace \texttt with \url if you are using the url package)
A paper with the same title will eventually appear, more focused on the theoretical aspects of the generation. Part of its content is cover in this talk presented at the AATG workshop of ICALP 2020.
Other versions of STGen
There exist other versions of STGen, in Java, Python, Julia, and Rust. Most of them are outdated and/or have poorer performance. The Rust version is perhaps the second-best (and less outdated) after the official C++ version presented here. If you don’t like C++, feel free to contact me to talk about the other versions.